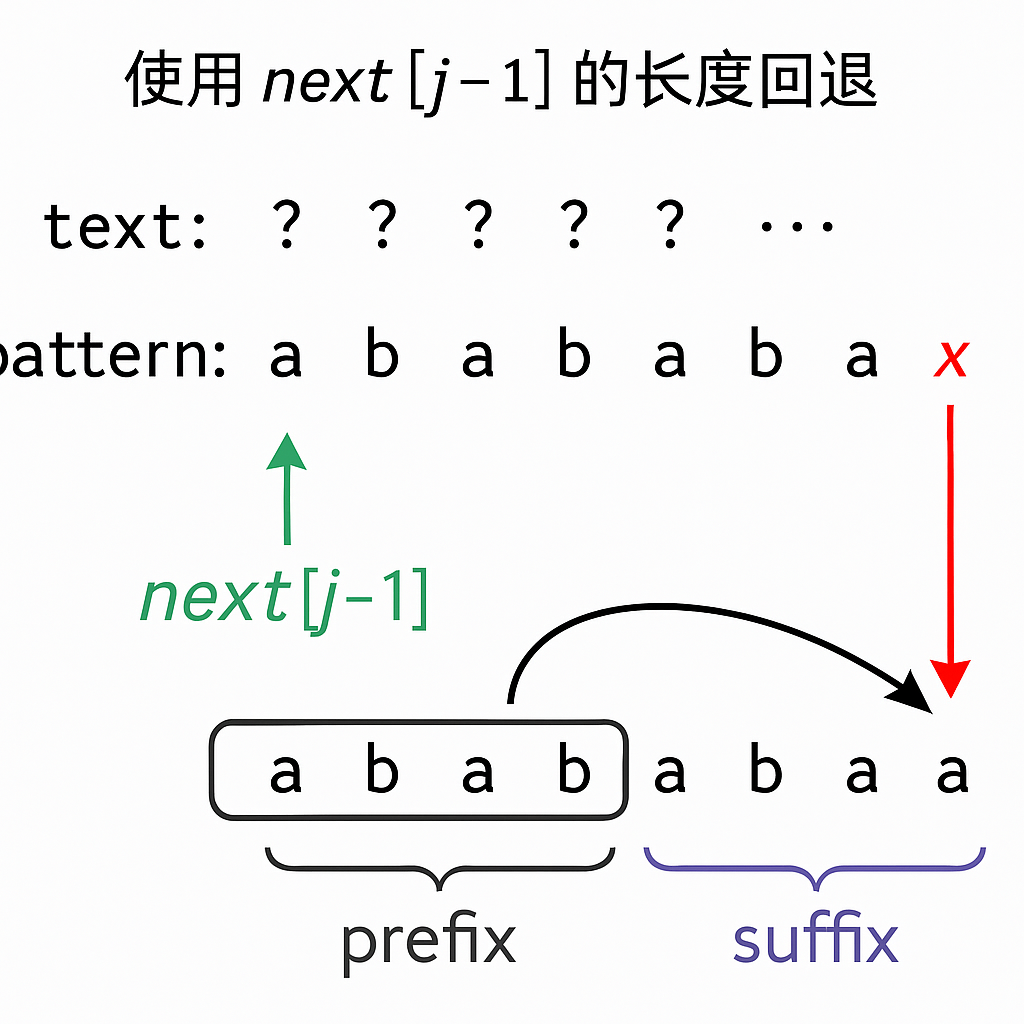
KMP算法之匹配过程详解——结构、原理与C++实现
学会构建 next 数组后,匹配过程就很简单,可以参照这篇博客。
KMP 利用已经部分匹配的信息,避免重复匹配,提高了字符串匹配的效率,时间复杂度是 $ O(n + m) $ ,其中 n 是主串长度,m 是模式串长度。
使用 next 数组做匹配
在文本串 s 里找是否出现过模式串 t 。定义两个下标 j 指向模式串起始位置, i 指向文本串起始位置。
那么 j 初始值为 0 , 因为 next 数组里记录的起始位置为 0。
i 就从0开始,遍历文本串,代码如下:
1 | for (int i = 0; i < s.size(); i++) |
接下来就是 s[i] 与 t[j] (因为 j 从 0 开始的) 进行比较。
如果 s[i] 与 t[j] 不相同,j 就要从 next 数组里寻找下一个匹配的位置。
代码如下:
1 | while(j > 0 && s[i] != t[j]) { |
如果 s[i] 与 t[j] 相同,那么 i 和 j 同时向后移动, 代码如下:
1 | if (s[i] == t[j]) { |
如何判断在文本串 s 里出现了模式串 t 呢,如果 j 指向了模式串 t 的末尾,那么就说明模式串 t 完全匹配文本串 s 里的某个子串了。
完整代码
1 | int j = 0; // 因为next数组里记录的起始位置为0 |
示例
文本串 s = "abcabcababac"
模式串 t = "ababac"
第一步:构造 next 数组
| i | t[i] | j(前缀指针) | 比较 | next[i] |
|---|---|---|---|---|
| 1 | b | 0 | a ≠ b | 0 |
| 2 | a | 0 | a = a | 1 |
| 3 | b | 1 | b = b | 2 |
| 4 | a | 2 | a = a | 3 |
| 5 | c | 3 | b ≠ c → 回退 j=next[2]=1 → a ≠ c → j=0 | 0 |
最终: next = [0, 0, 1, 2, 3, 0]
第二步:匹配过程
文本串 s = "abcabcababac"
模式串 t = "ababac"
初始状态:i = 0, j = 0
i |
s[i] |
t[j] |
匹配 | j 变化—-本轮执行后 j 的值 |
说明 |
|---|---|---|---|---|---|
| 0 | a | a | 是 | j=1 | 首字符匹配 |
| 1 | b | b | 是 | j=2 | |
| 2 | c | a | 否 | j=0 | 回退 j = next[j - 1] = next[1] = 0 |
| 2 | c | a | 否 | j=0 | 继续下一轮匹配 |
| 3 | a | a | 是 | j=1 | |
| 4 | b | b | 是 | j=2 | |
| 5 | c | a | 否 | j=0 | 再次失败,回退 |
| 6 | a | a | 是 | j=1 | |
| 7 | b | b | 是 | j=2 | |
| 8 | a | a | 是 | j=3 | |
| 9 | b | b | 是 | j=4 | |
| 10 | a | a | 是 | j=5 | |
| 11 | c | c | 是 | j=6 | 完全匹配成功 |
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 chengoasis!