KMP字符串匹配算法之next数组详解——结构、原理与C++实现
核心思想是: 在匹配失败时尽量减少主串指针的回退,从而提高匹配效率。
一句话总结: KMP 利用已经部分匹配的信息,避免重复匹配,提高了字符串匹配的效率,时间复杂度是 $ O(n + m) $ ,其中 n 是主串长度,m 是模式串长度。
KMP 算法结构
KMP 算法包含两个核心部分:
- 构建“部分匹配表”(又称 next数组 或 前缀函数表)
- 利用 next 数组进行字符串匹配
核心概念:next数组
next[i] 表示:模式串 pattern[0...i] 的最长相等的前缀和后缀的长度
作用:当匹配失败时,模式串可以跳过哪些已经匹配过的字符。
示例
- 前缀:除了最后一个元素以外,字符串的所有头部子串
- 后缀:除了第一个元素以外,字符串的所有尾部子串
- 部分匹配值PM为字符串的前缀和后缀的最长相等的前后缀长度
模拟KMP算法求next数组: 以 ababa 为例求 PM 和 next 数组
| 模式串(pattern[0:i]) | 前缀 | 后缀 | 最大相同前后缀长度 | PM值(部分匹配值) | next[i] |
|---|---|---|---|---|---|
| a | 空 | 空 | 0 | 0 | 0 |
| ab | a | b | 0 | 0 | 0 |
| aba | a、ab | ba、a | 1 | 1 | 1 |
| abab | a、ab、aba | bab、ab、b | 2 | 2 | 2 |
| ababa | a、ab、aba、abab | baba、aba、ba、a | 3 | 3 | 3 |
这里默认
next数组下标从0开始当
next数组下标从0开始时,next[i]实际就是 PM 值(部分匹配值)next[0]的值并不会被使用,所以它设为0或-1不影响算法正确性
思考为什么 next[0] 的值没有任何影响?
情况一:
next[0] = 0(现代主流写法)- 适用于多数教材 / 面试代码。
- 匹配失配时,回退到
pattern[0]重新开始。
1
i = next[i - 1] = next[0] = 0; // 代表“回退到模式串开头”,从头继续匹配,这是合法的、正常的回退策略。
情况二:
next[0] = -1(老式写法)- 一种更激进的策略,直接跳出当前字符匹配。
1
2
3while (i != -1 && pattern[i] != text[j]) {
i = next[i];
}- 当
i = 0且失配,变成i = next[0] = -1,代表无法继续匹配,跳到初始状态。 - 这是一种优化写法,可以减少边界判断。
next[0] 是会被用到的,但它的值设为 0 或 -1 都是合法的,只是代表不同的回退策略。
代码实现:构造 next 数组
1 | // 构建 KMP 的 next 数组(下标从 0 开始) |
- 时间复杂度:$ O(m) $ ,
m是模式串pattern的长度 - 空间复杂度:$ O(m) $
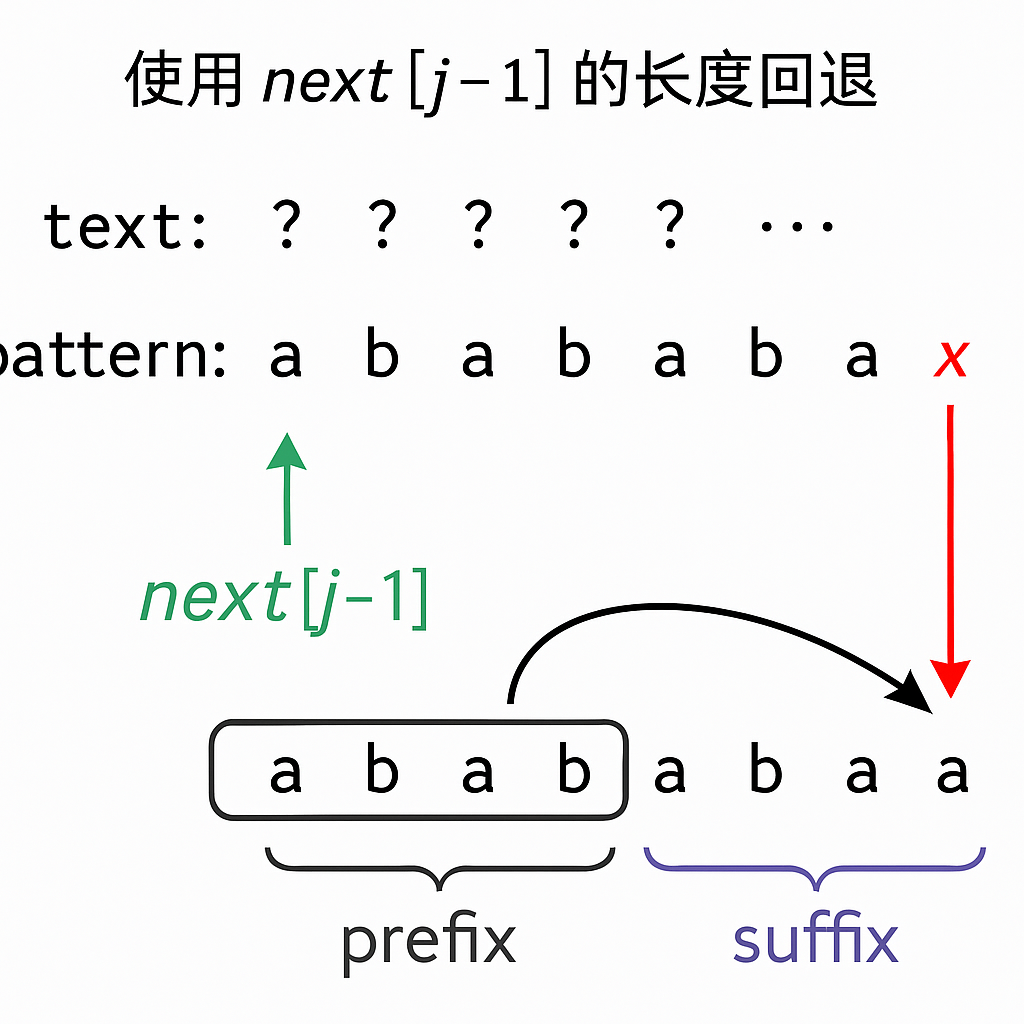
什么是 next[j-1]
next[j-1]表示的是 模式串 pattern 的前缀 pattern[0~j-1] 中,最长的相等“前缀=后缀”的长度 。- 换句话说:如果当前
pattern[i] != pattern[j],说明在j-1位置处构建的“前缀”不能继续往后匹配了。 - 那怎么办?我们就尝试让这个前缀缩短成一个更短但相同尾部的子前缀,继续尝试匹配

本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 chengoasis!