LeetCode 59.螺旋矩阵II

题目描述

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1:

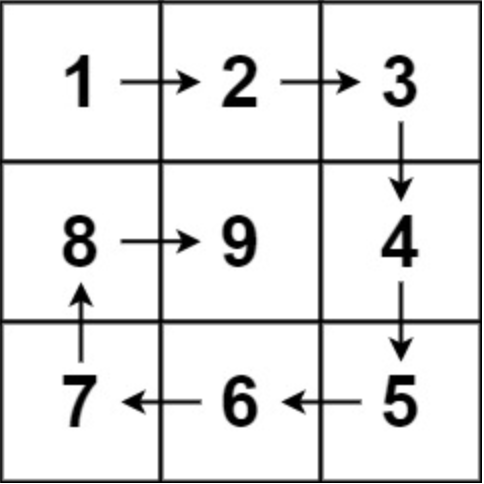
输入: n = 3
输出: [[1,2,3],[8,9,4],[7,6,5]]

示例 2:

输入: n = 1
输出: [[1]]

提示：

$1 \le {n} \le 20$

思路

本题并不涉及到什么算法，就是模拟过程

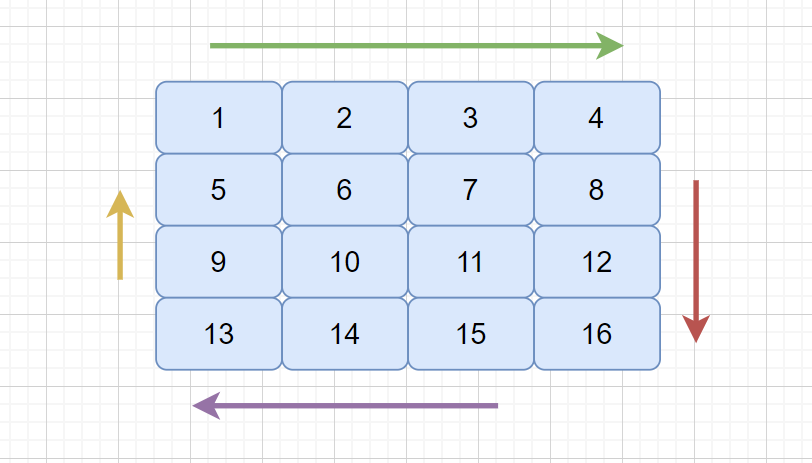
**模拟顺时针画矩阵的过程：**由外向内一圈一圈这么画下去

填充上行从左到右
填充右列从上到下
填充下行从右到左
填充左列从下到上

给出 n , 会填充 n*n 个元素到数组中，所以这个二维矩阵一定是一个正方形。

可以使用变量 cnt 来表示当前所需要填充的元素，同时也作为循环的控制条件。当 cnt 大于 n 时跳出循环。

C++代码

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> ans(n, vector<int>(n)); 
        int left = 0, right = n - 1;
        int top = 0, bottom = n - 1;
        int cnt = 1;
        while (cnt <= n * n) {
            for (int i = left; i <= right; ++i) {
                ans[top][i] = cnt++;
            }
            ++top;
            for (int i  = top; i <= bottom; ++i) {
                ans[i][right] = cnt++;
            }
            --right;
            for (int i = right; i >= left; --i) {
                ans[buttom][i] = cnt++;
            }
            --bottom;
            for (int i = bottom; i >= top; --i) {
                ans[i][left] = cnt++;
            }
            ++left;
        }
        return ans;
    }
};

时间复杂度：$O(n^2)$
空间复杂度：$O(1)$ , 除了输出数组以外，空间复杂度是常数。

LeetCode 54.螺旋矩阵II

题目描述

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1:

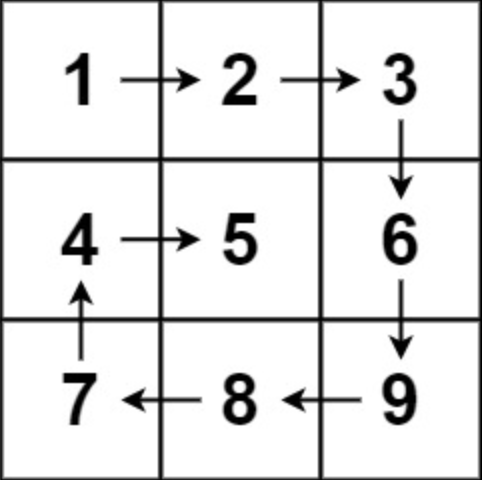
输入: matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出: [1,2,3,6,9,8,7,4,5]

示例 2:

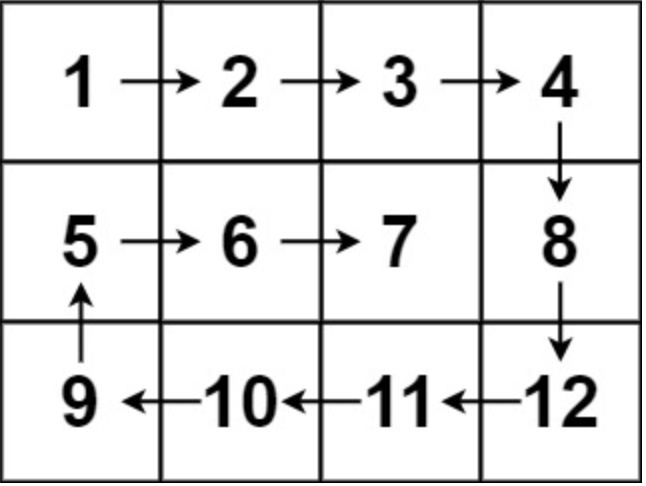
输入: matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出: [1,2,3,4,8,12,11,10,9,5,6,7]

提示：

$m == matrix.length$
$ n == matrix[i].length $
$ 1 \le {m, n} \le 10$
$ -100 \le matrix[i][j] \le 100$

思路

思路跟上题一样，不过是反过来了。

模拟顺时针扫描矩阵的过程： 由外向内一圈一圈扫描下去

扫描上行从左到右
扫描右列从上到下
扫描下行从右到左
扫描左列从下到上

给出了二维矩阵 matrix ，该矩阵可能是正方形也可能是长方形。跟上题唯一不同的是需要注意是否发生越界，因为上题中矩阵一定是正方形的，最后一次循环完要么是中间的一层，要么是中建的一个点，不会发生越界和重复填充。

该题中矩阵可能是长方形的，可能会发生数组越界（返回矩阵 ans 的大小为 len ）

C++代码

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        int len = m * n;
        vector<int> ans(len);
        int left = 0, right = n - 1;
        int top = 0, bottom = m - 1;
        int index = 0;    // 用来记录当前存储在 ans 中的位置
        while (index < len) {
          	// 注意每个 for 循环中都需要判断index < len, 否则可能出现越界的情况
          	// 如果矩阵是正方形的就不需要判断这种情况，但是这题中矩阵可能是长方形的，请自己手动模拟一下
            for (int i = left; i <= right && index < len; ++i) {
                ans[index++] = matrix[top][i];
            }
            ++top;
            for (int i = top; i <= bottom && index < len; ++i) {
                ans[index++] = matrix[i][right];
            }
            --right;
            for (int i = right; i >= left && index < len; --i) {
                ans[index++] = matrix[bottom][i];
            }
            --bottom;
            for (int i = bottom; i >= top && index < len; --i) {
                ans[index++] = matrix[i][left];
            }
            ++left;
        }
        return ans;
    }
};

时间复杂度：$O(mn)$ , 其中 m 和 n 分别是输入矩阵的行数和列数。矩阵中的每个元素都要被访问一次。
空间复杂度：$O(1)$ , 除了输出数组以外，空间复杂度是常数。